Inhalt
-
Algebra
- Bruchrechnung
- Einheiten
- Grundrechenarten
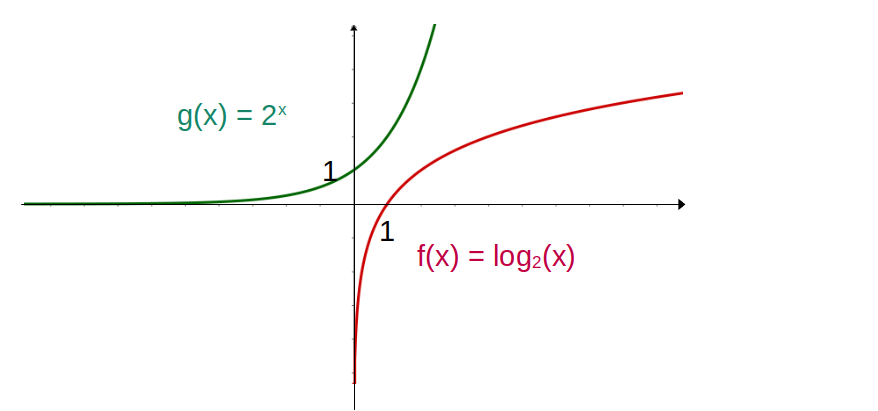
- Logarithmus
- PotenzWurzel
- Rechengesetze
- Zahlen
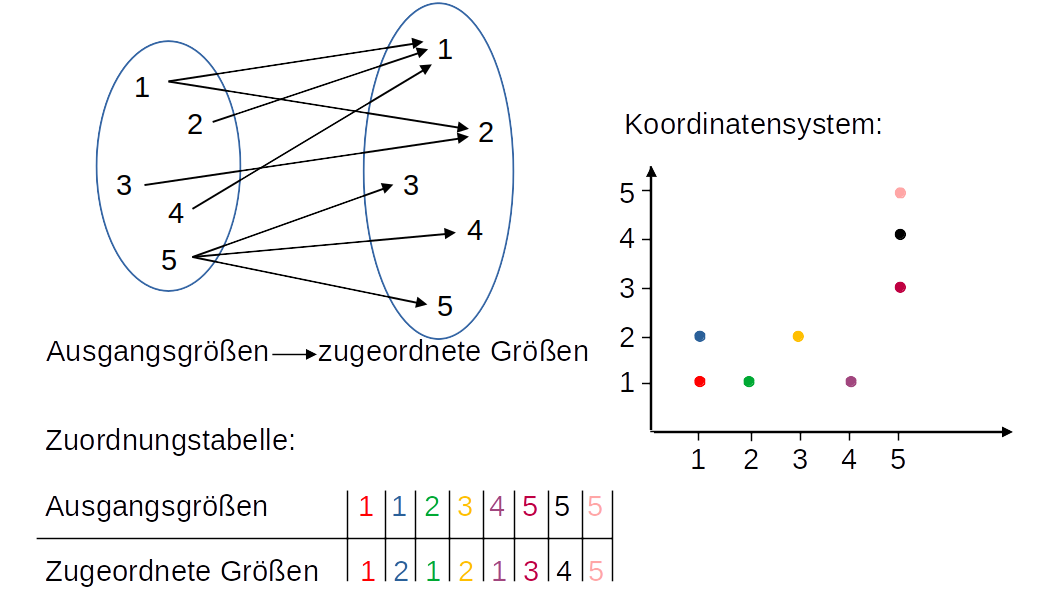
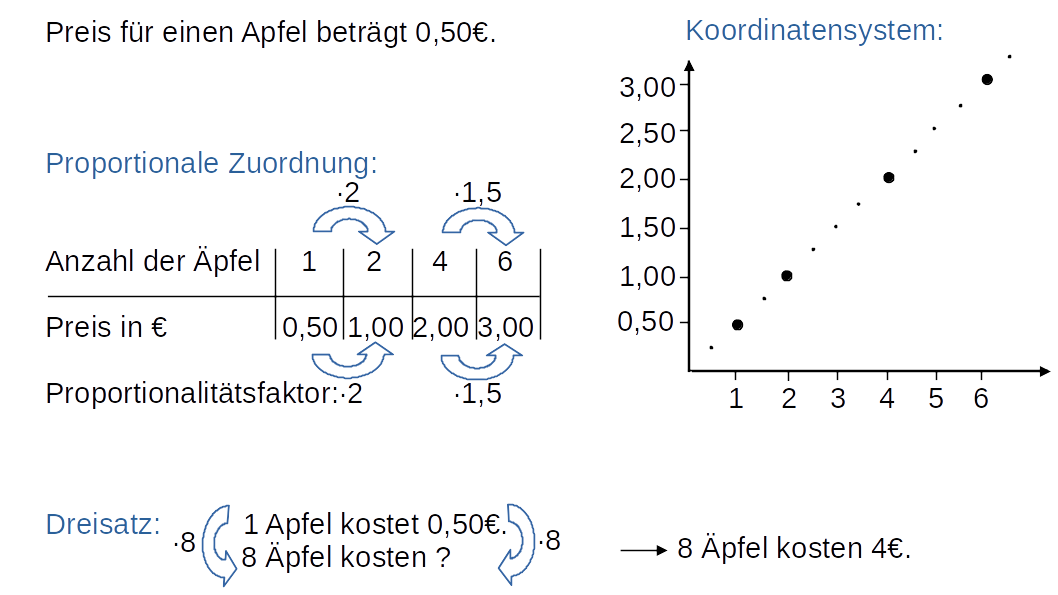
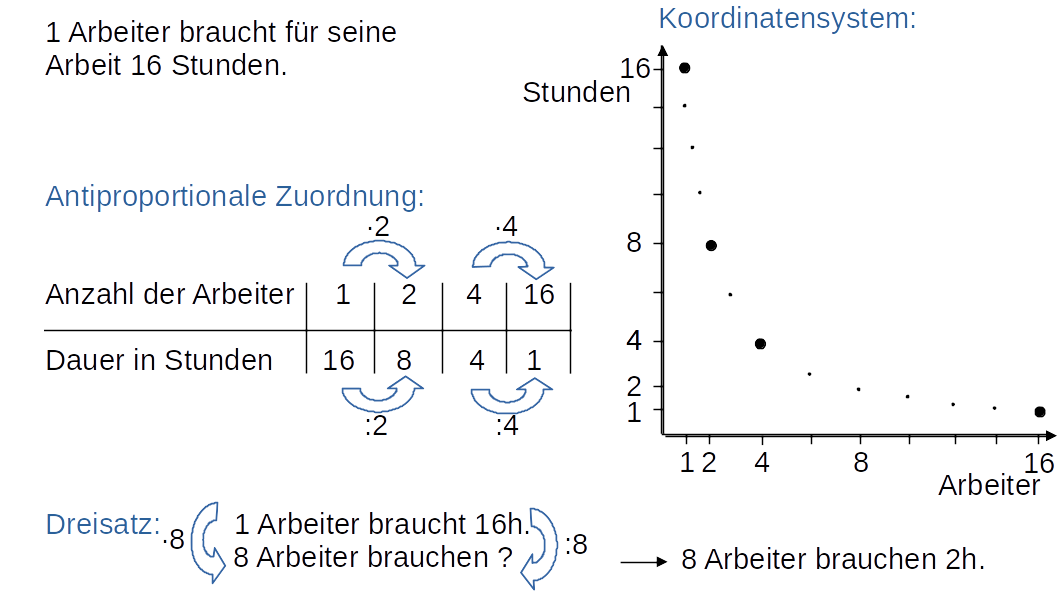
- Zuordnung
-
Geometrie in der Ebene
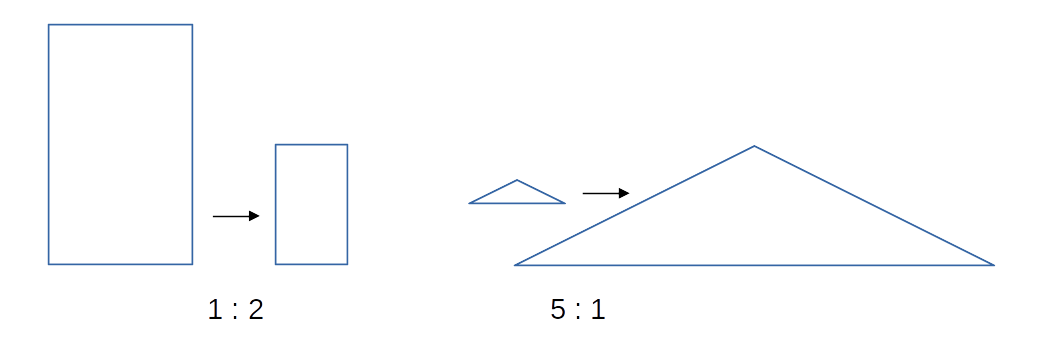
- Maßstab
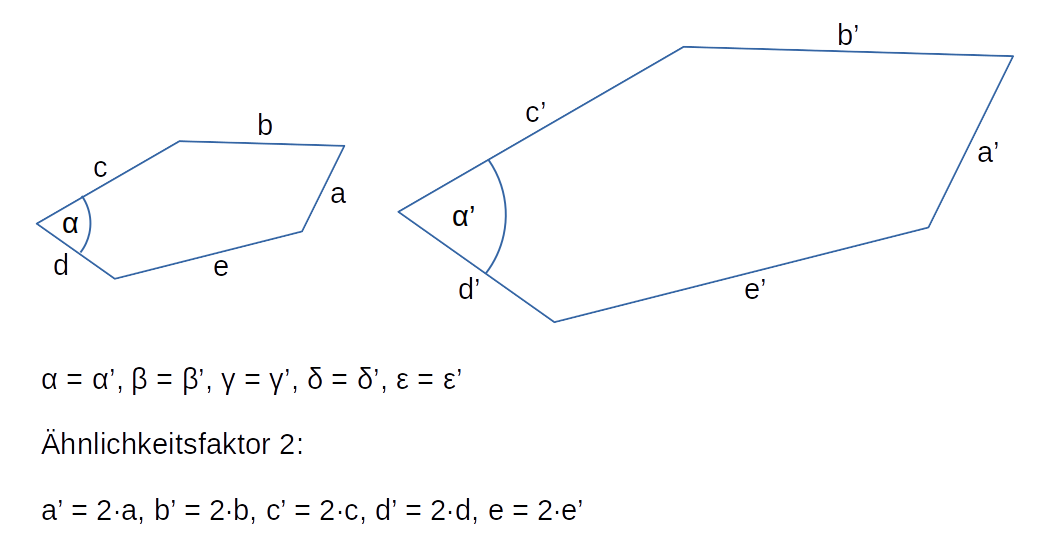
- Ähnlichkeit von Vielecken
- Ähnlichkeitssatz für Dreiecke
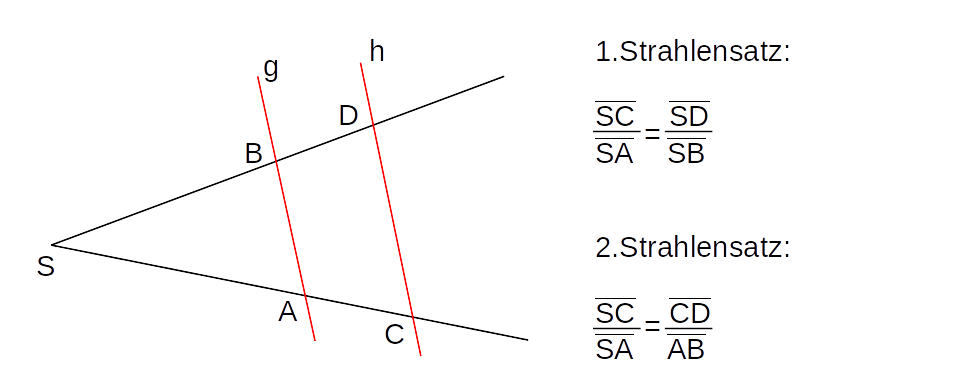
- 1.Strahlensatz
- 2.Strahlensatz
- >Zentrische Streckung
- Dreieck
- Fläche und Umfang
- Kreis
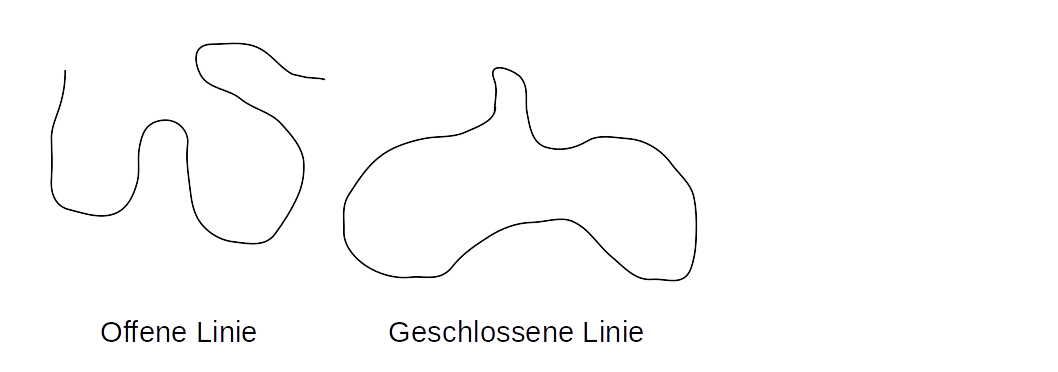
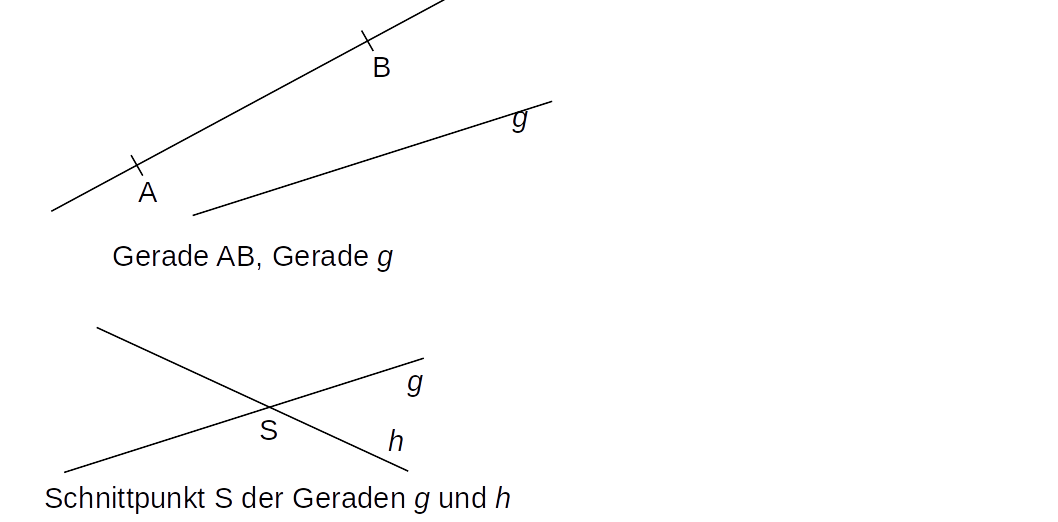
- Linien
- Transformationen
-
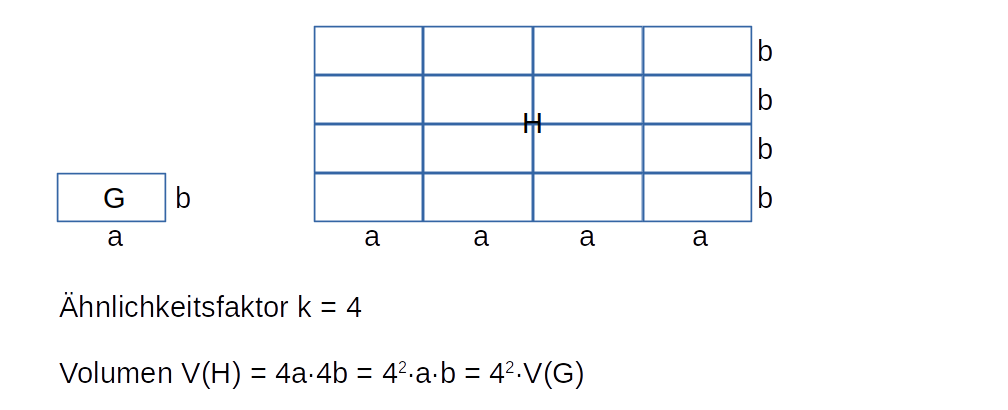
Ähnlichkeit
-
Geometrie im Raum
- Vektoren
- Volumen und Oberfläche
-
Analysis
- Ableitung
- Folgen
- Kurvendiskussion
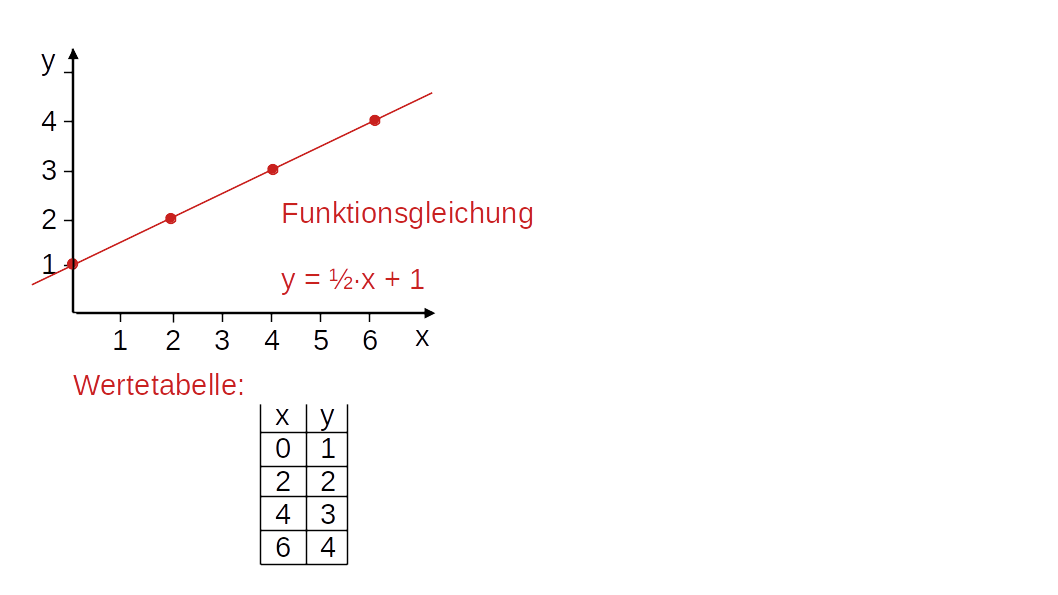
- Lineare Funktion
- Quadratische Funktion
-
Stochastik
| Unterstufe | Mittelstufe | Oberstufe | +++
Kontakt:
B.El Ernst
gigageo.de verfolgt keinerlei kommerzielle Absichten.
Haftung für Inhalte
Alle Inhalte meines Internetauftritts wurden mit größter Sorgfalt und nach bestem Gewissen erstellt. Für die Richtigkeit, Vollständigkeit und Aktualität der Inhalte kann ich jedoch keine Gewähr übernehmen.
Haftungsbeschränkung für externe Links
Meine Webseite enthält keine Links auf externe Webseiten Dritter.
Urheberrecht
Die Inhalte auf meiner Webseite unterliegen dem deutschen Urheberrecht. Die Vervielfältigung, Bearbeitung, Verbreitung und jede Art der Verwertung bedürfen der vorherigen Zustimmung des jeweiligen Urhebers i.S.d. Urhebergesetzes. Downloads und Kopien dieser Seite sind nur für den privaten und nicht kommerziellen Gebrauch erlaubt. Sind die Inhalte auf meiner Webseite nicht von mir erstellt worden, sind die Urheberrechte Dritter zu beachten. Die Inhalte Dritter werden als solche kenntlich gemacht. Falls Ihnen trotzdem eine Urheberrechtsverletzung auffallen sollte, bitte ich um einen entsprechenden Hinweis. Bei Bekanntwerden von Rechtsverletzungen werde ich derartige Inhalte unverzüglich entfernen.
Der Schutz Ihrer Daten ist mir wichtig.
Lesen Sie hier mehr dazu.
Name des Verantwortlichen
B.El Ernst
Bereitstellung der Website und Erstellung von Logfiles
Als Provider der Webseite erhebt und speichert strato.de automatisch Informationen
in sogenannten Server-Log-Dateien, die Ihr Browser automatisch an ihm übermittelt. Dazu gehören:
Verwendung von Cookies
Ich verwende keine Cookies.
Speicherung personenbezogener Daten bei Kontaktaufnahme
Sofern Sie per E-Mail den Kontakt mit mir aufnehmen, werden die von Ihnen übermittelten personenbezogenen Daten automatisch gespeichert. Diese Daten werden für Zwecke der Bearbeitung Ihres Anliegens und der Kontaktaufnahme mit Ihnen gespeichert. Die Löschung der Daten erfolgt, sobald deren Speicherung für die Bearbeitung Ihres Anliegens nicht mehr erforderlich ist.
Impressum
E-Mail: info@gigageo.de
Datenschutz
info@gigageo.de
Eine Speicherung dieser Daten zusammen mit anderen personenbezogenen Daten des
Nutzers findet nicht statt. Zweck der Datenspeicherung ist die technische Optimierung meiner Internetseite. Rechtsgrundlage für die vorübergehende Speicherung der Daten ist
Art. 6 Abs.1 lit.f DSGVO. Die Daten werden für zwei Monate gespeichert, sie
werden lediglich statistisch ausgewertet.
Details zu den Datenschutzbedingungen unseres Providers finden Sie unter
https://strato.de/blog/tag/datenschutz/.

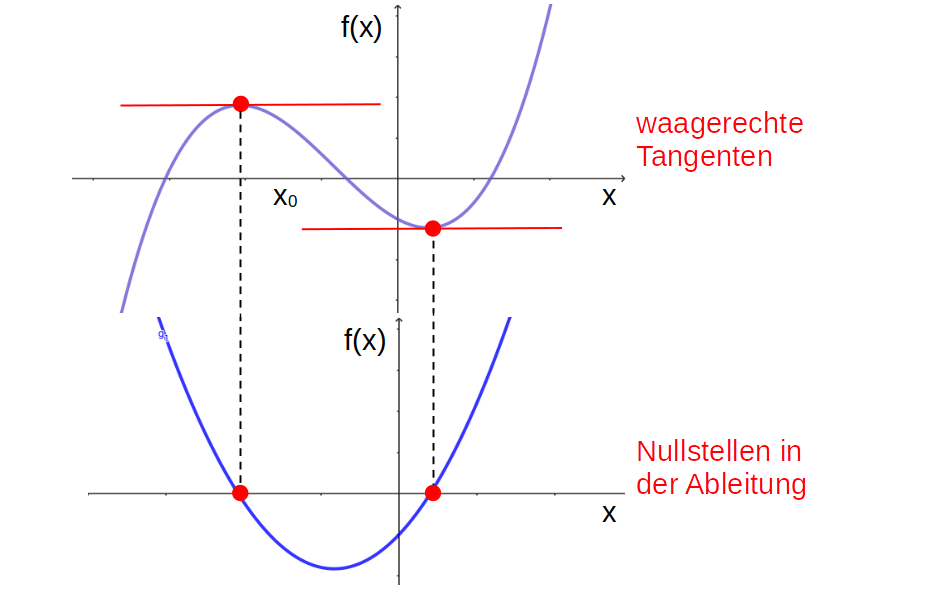
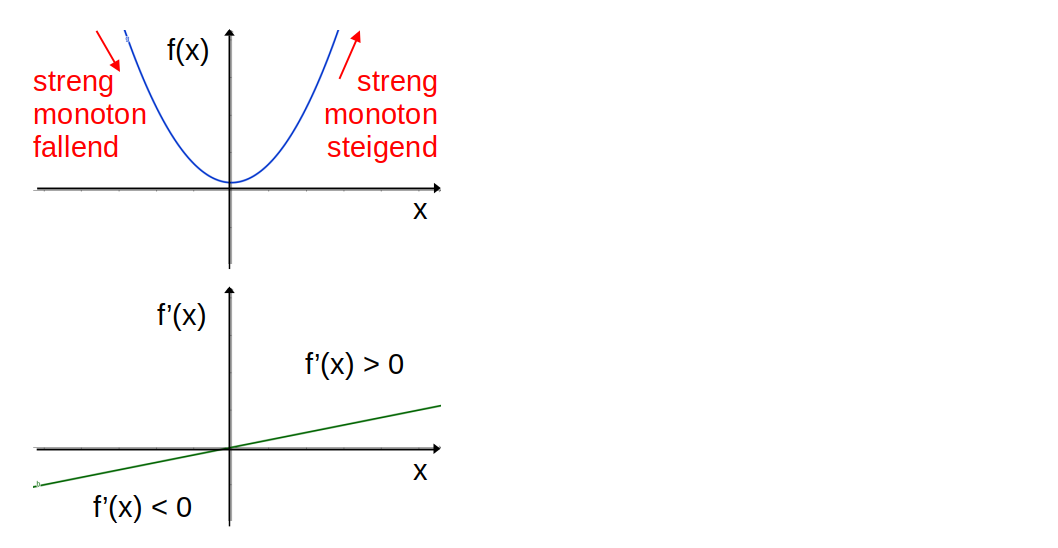
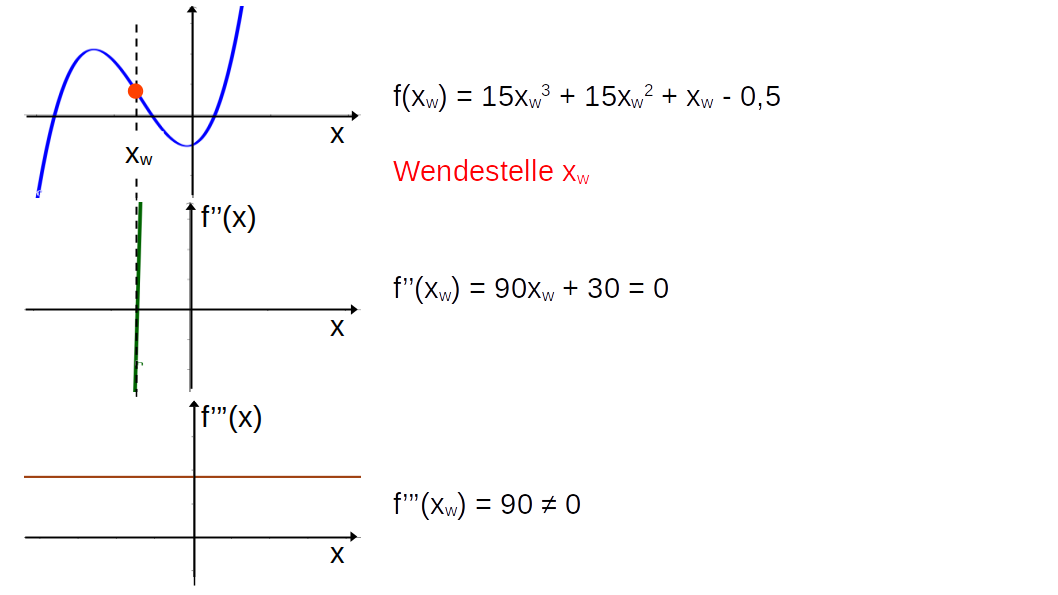
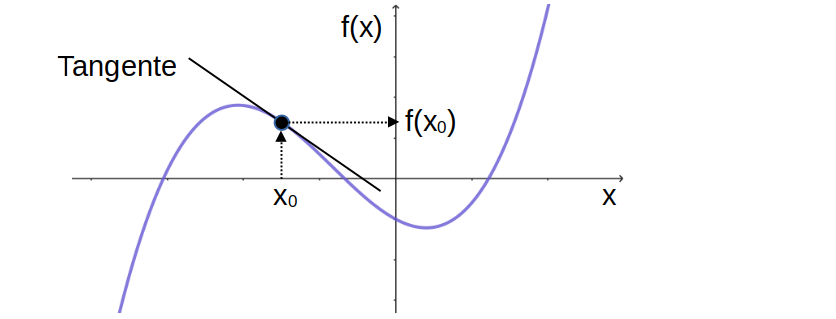 Die Ableitungsfunktion \(f'\) zu einer Funktion \(f\) ist die "Funktion der Tangentensteigungen": An jeder Stelle \(x\) hat die Steigung der Tangente an
den Graphen von \(f\) einen Wert, der der Ableitung der Funktion \(f'\)
entspricht.
Die Ableitungsfunktion \(f'\) zu einer Funktion \(f\) ist die "Funktion der Tangentensteigungen": An jeder Stelle \(x\) hat die Steigung der Tangente an
den Graphen von \(f\) einen Wert, der der Ableitung der Funktion \(f'\)
entspricht.





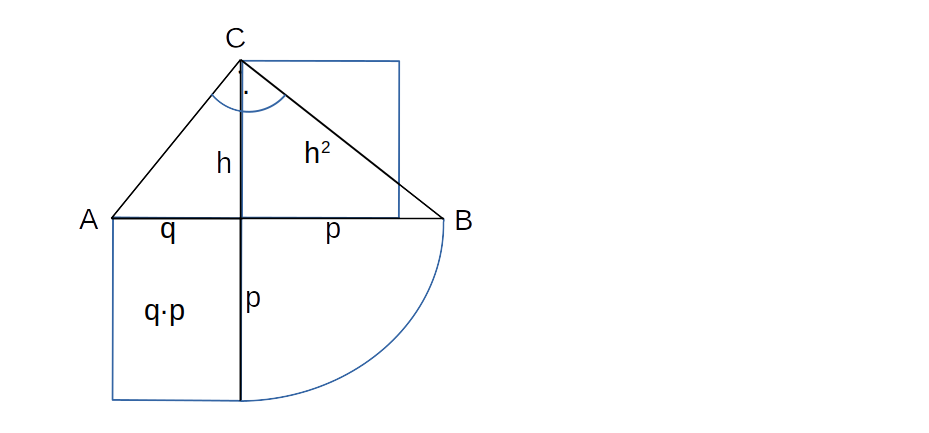



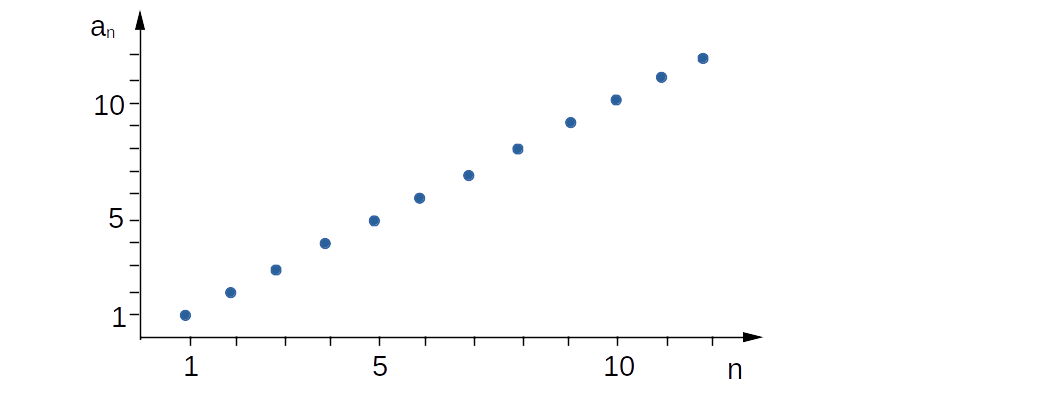
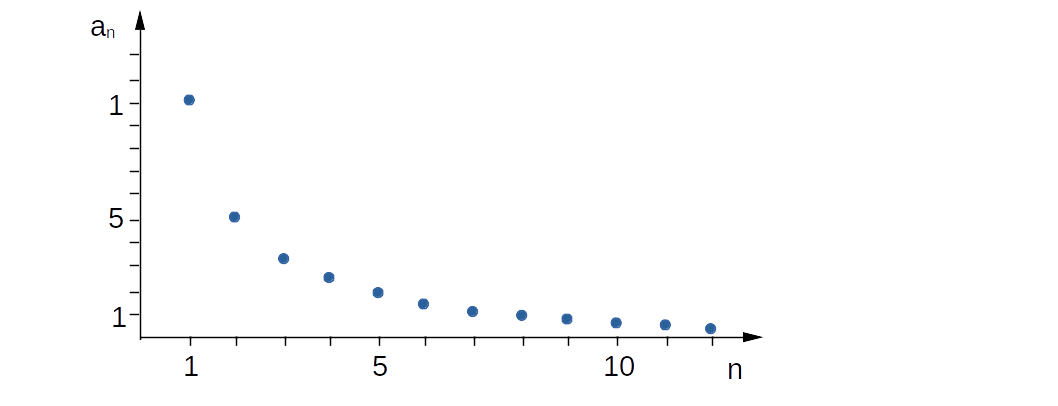
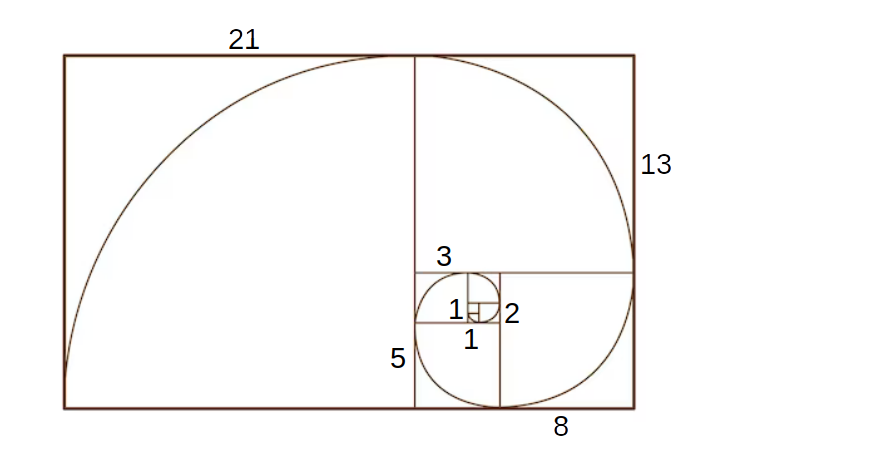 Zeichnet man die Verbindung als Kurve, so erhält man
eine Spirale, die in der Natur häufig vorkommt: Schnecken,
Wirbelstürmen, Blumen, Galaxien.
Zeichnet man die Verbindung als Kurve, so erhält man
eine Spirale, die in der Natur häufig vorkommt: Schnecken,
Wirbelstürmen, Blumen, Galaxien.





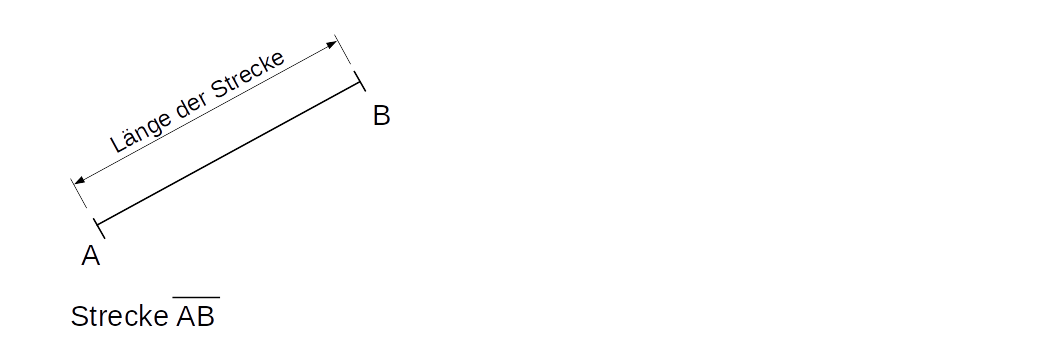








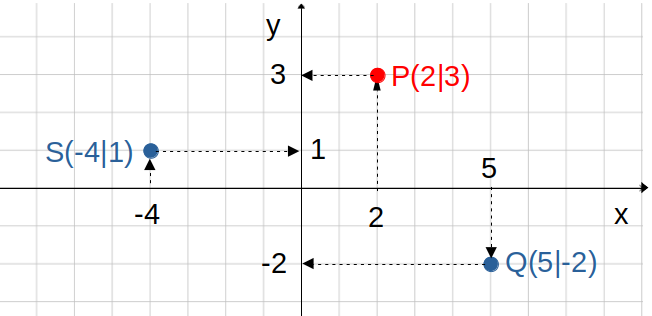 Der Punkt \(P(2|3)\) hat die 1.Koordinate
\(2\) und die 2.Koordinate \(3\).
Der Punkt \(P(2|3)\) hat die 1.Koordinate
\(2\) und die 2.Koordinate \(3\).
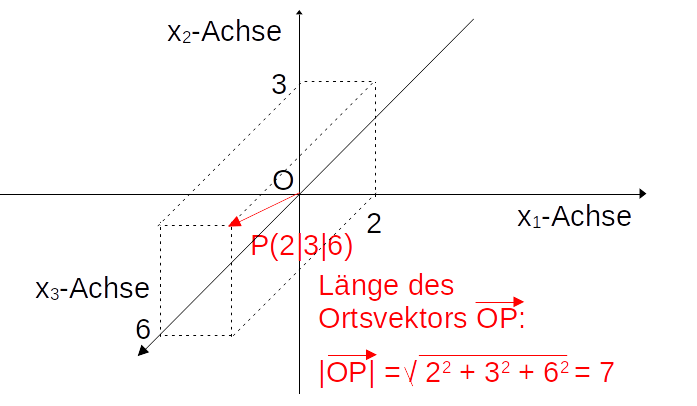
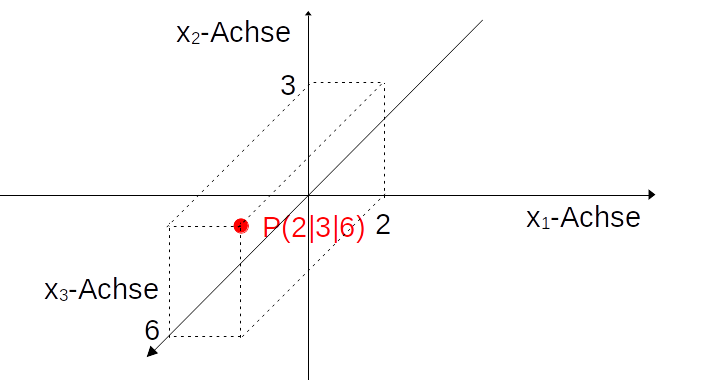 Der Punkt \(P(2|3|6)\) hat die 1.Koordinate
\(2\), die 2.Koordinate \(3\) und die 3.Koordinate \(6\).
Der Punkt \(P(2|3|6)\) hat die 1.Koordinate
\(2\), die 2.Koordinate \(3\) und die 3.Koordinate \(6\).